• May 12, 2015
• 7,569 views
• Short URL: rvarg.as/line/

Modelling Line of Balance Schedules with Start-Finish Relationships

Ricardo Viana Vargas
United Nations (UNOPS) / Universidade Federal Fluminenses
Felipe Fernandes Moreira
Universidade Federal do Ceará

You can download the exhibits as Microsoft Project 2010 files (.mpp) Download Exhibits

Abstract

The use of the Line of Balance Scheduling Method (LBSM) has been increasing, especially by construction industry companies in Brazil, Finland and Australia. The method addresses to the particularities of construction projects more effectively than the Critical Path Method does. One drawback of the method is the unavailability of commercial software featuring the fundamentals of LBSM. Studies pointed this as a factor that prevents a more frequent use. Recognizing the potential of the method for managing construction projects, the objective of this paper is to propose methodologies for modelling Line of Balance schedules using CPM software. In order to model the schedule, the paper demonstrates the use of the “Start-Finish” logic relationship and its contributions for two different approaches for the modelling: Network and Linear Scheduling Approach. The first approach demonstrate the design of a CPM network, which simulates the structure and function of a Line of Balance, with the objective of benefiting from CPM calculations. The second approach drops the CPM calculations and focuses on modelling, tuning and balancing individual workflow lines to and from milestones activities.

Introduction

Part of the planning effort in a project is directed toward determining the sequence of the activities in such a way that the execution goes on in the most efficient way possible. This sequencing is modeled using relationships between activities, called dependencies, which may be “finish-start” (“FS”), “start-start” (“SS”), “finish-finish” (“FF”) and “start-finish” (“SF”). This link establishes a relationship between activities, where one of them is the predecessor (the activity that comes before logically) and the other is the successor (the activity that comes after logically) [10].

The Line of Balance Scheduling Method (LBSM) is a technique absent from the PMBOK® Guide since its first release in 1996 through the current 2013 edition; CPM network scheduling is the most prominently discussed [12,13]. This omission ignores a current trend in the construction industry. Civil construction companies from Brazil, Finland and Australia are satisfactorily using the LBSM [3]. Employing this technique is related to the efforts to incorporate concepts of Lean Construction into company project management systems, more precisely with the Last Planner® production system, developed by Glenn Ballard and Greg Howell, founders of the Lean Construction Institute® (LCI) [1].

The US Navy initially used the concept of Line of Balance as a technique for planning the execution of activities of the industry in 1942 [5]. General Electric later, working for the US Navy, used it not only as a planning tool but also as a controlling tool. In the United Kingdom, the method was adopted by the Nation Building Agency.

According to Shaikh, the increasing usage of LBSM (one that receives the most attention among others techniques) comes in recent years, when an increasing demand for cost control and resource optimization has forced schedules (and schedulers) to focus on more than just the critical path. He attributes the limited usage of the technique to the lack of powerful and user-friendly computer applications. The author insists that the most commonly accepted commercial scheduling software packages are based on the CPM using the precedence diagramming method as the network analysis algorithm [12].

Mubarak, writing about Linear Schedule Methods (LSM), recognizes the same phenomenon of the lack of acceptance in the construction industry despite its analytical advantages. The author considers a drawback the fact that there are no major software packages offering LSM capabilities. Mubarak affirms that the LSM is poised to be make a comeback, since many software packages are becoming available [7]. Zack Jr. and Collins reveal a survey from the UK construction industry that only 1% of the respondent companies use the Line of Balance, while 54% use bar charts [13].

The preference for the Line of Balance scheduling method for developing the project schedule is due to the fact that the “unit of production x time” configuration, instead of the usual Gantt chart configuration (“activities x time”), results in better visualization for the link between the flow of work of the different crews [1]. This allows a different perspective for the control of the project activities – with the Line of Balance, the focus of control is the rate of production of the working crews and not the control of individual discrete activities, which is the focus of the Critical Path Method, largely used [5].

Objectives

1 Microsoft® is either registered trademark or trademark of Microsoft Corporation in the United States and/or other countries.

The LBSM offers a new perspective for construction project management and a potential for improving performance. Taking into account the diagnosis of the authors referenced above, the objective of this paper is to propose the modelling of a Line of Balance schedule using an acclaimed CPM based scheduling software, like Microsoft®1 Project. In order to demonstrate this proposal, it is important to study how this method works.

In order to model the Line of Balance with CPM based structures, the most uncommon precedence relationship between activities, the “start-finish” relation may be utilized. Kerzner classifies the “SF” relation as the “least common type of precedence chart” [6]. Referring to the construction industry, Mubarak considers the “SF” logic relationships “uncommon” and “almost nonexistent”, recognizing the other three as “useful” and “common” [7].

The PMBOK® Guide (2013) defines the “SF” logical relationship as “the completion of the successor activity depends upon the initiation of the predecessor activity ” [10]. It is only cited to give a complete representation of all possible links, since this is considered a rare relationship. The first and second editions of PMBOK even advise project managers not to use relationships other than the most usual (finish-start), since they may cause “unexpected results”[9].

It is important to note that, when working with “Start-Finish” logical relationships, the predecessor is not the activity that happens chronologically before, while the successor is not the activity that happens chronologically after. The predecessor (the activity that comes before logically) and the successor (the activity that comes after logically) [10].

The main objective of this paper is to propose how to model a Line of Balance schedule, while the secondary objective is to investigate the “unexpected results” of this sort of modelling.

Line of Balance Scheduling Method

Zack Jr. and Collins [13] define a Line of Balance schedule as a graphical display of scheduled units versus actual units over a given set of critical schedule control points on a particular day. Shaikh defines the Line of Balance as a graphical variant of the linear scheduling methods which considers an activity location as a dimension in the planning, thereby allowing the balancing of operations for continuous and efficient use [12]. This definition is similar to the one given by Kenley and Seppänen [5].

The Line of Balance proposes that the planning of the activities should be according to a rate of production, or cycle, meaning the number of production units delivered by a working crew, over a certain time [4]. Such concept is similar to the concept of takt-time from the Toyota Production System, a measure of time between two outputs in a production system [8].

An example showing a comparison of the regular Gantt chart and the Line of Balance for scheduling three tasks repeating itself continuously along four floors is presented as Exhibits 1, 2 & 3. The assumption is that the next task initiates when the working crew ends the task on the preceding production unit.

Exhibit 1 – List of Activities

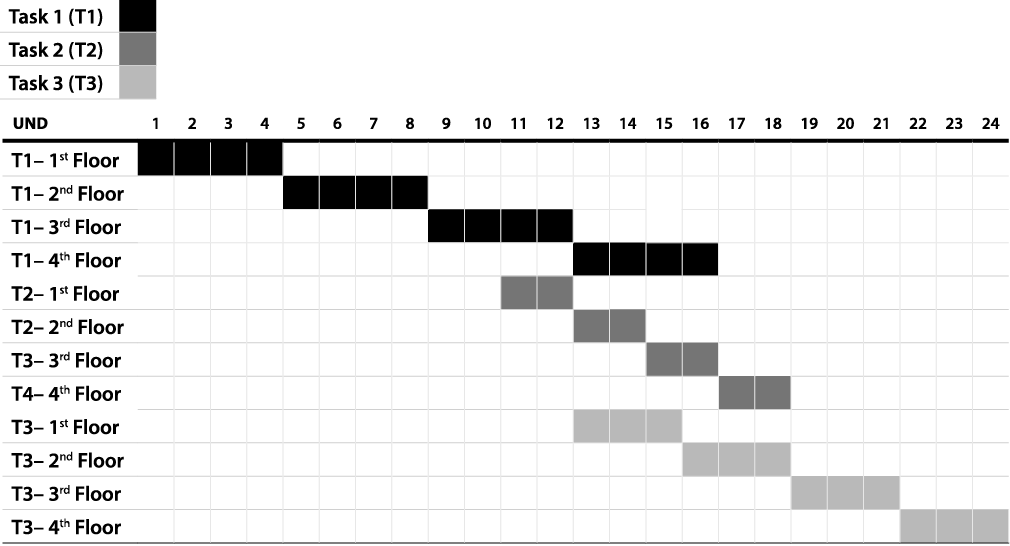Exhibit 2 – Schedule Using the Gantt Chart

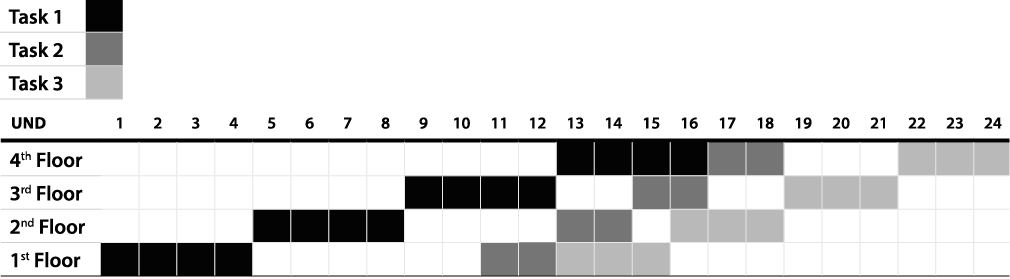Exhibit 3 – Schedule Using the LBSM

The rate of production, or cycle, is the slope of each line (Exhibit 2 and 3). For Task 1 the cycle is 0.25 units per unit of time, for Task 2 the cycle is 0.50 units per unit of time and for Task 3 the cycle is 0.33 units per unit of time. The analysis of these cycle times allows the management team to balance the lines to optimize the use of resources and achieve a reduction of the time needed to complete the project. Exhibit 4 shows the result of reducing the amount of resources of Task 2 by half (in other words, reducing its cycle time to 0.25, the same value of Task 1, and increasing the Task 2 duration from two days to four days per floor).

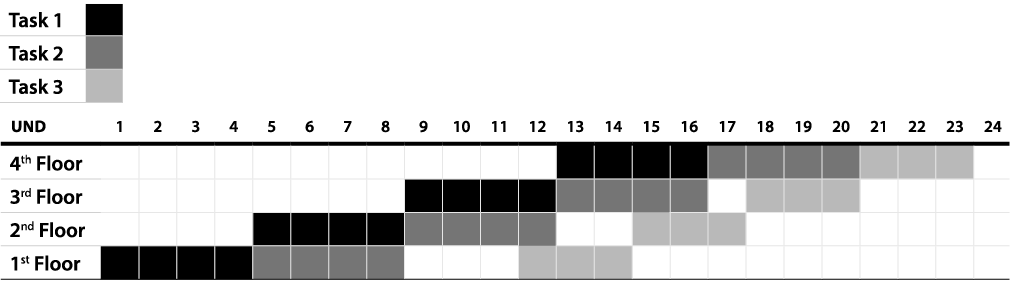Exhibit 4 – Balancing Lines to Achieve a Schedule Reduction

The line balancing of these two activities allowed the project completion to happen one day earlier with the reduction of the resources used on Task 2 only – the remaining tasks were left untouched. The comparison of the Gantt chart and the Line of Balance also shows a significant reduction in the number of lines displayed on the schedule (from twelve in the Gantt chart to four in the Line of Balance). The large reduction on the example shows the potential to simplify the schedule chart of a real project that contains several repetitive processes like, for example, a building with 100 floors with “n” different kinds of tasks in each floor. The simplification factor is the number of tasks inside each repetitive process (also called production unit). If you have 100 km of road and 20 tasks for each km, by using the Line of Balance, you are reducing the number of lines of your Gantt chart by 20 (Eq. 1).

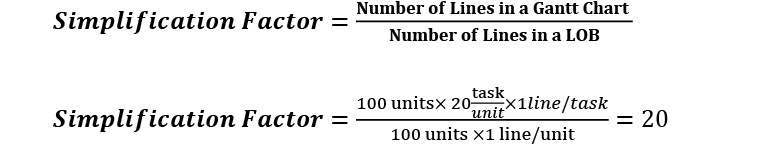EQ 1 – Simplification Factor

It is important to note that even though the example used cycle of tasks, it is possible to model a Line of Balance with process cycles, deliverables and sub-nets of precedency diagrams [5]. In addition, the example used floors, but it can also be used for houses, apartments, locations of a building floor, linear sections of a highway or pipeline, etc.

In the civil construction industry, the repetition of activities is commonly scheduled continuously [5]. Exhibit 6 shows the activities listed in Exhibit 1 modeled without the constraint of continuous repetition.

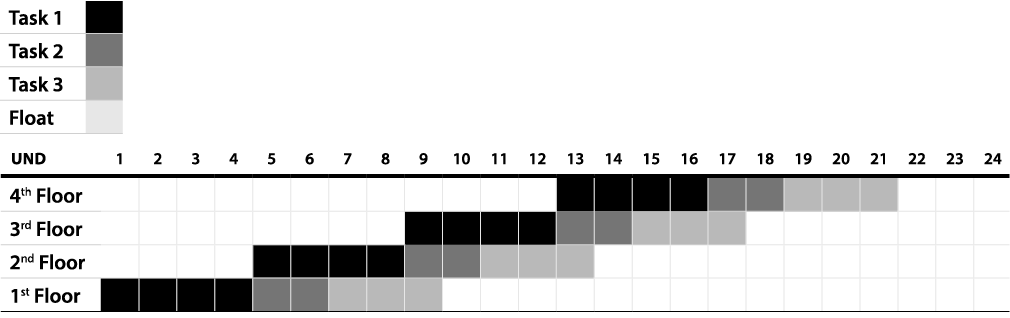Exhibit 5 – Line of Balance Without the Continuity of Repetition

On the resulting Line of Balance, the sequence of tasks is finishing on the 21st day (3 days earlier). This happens because there is now a lack of continuity in the Task 2 and Task 3 lines. The new configuration presents a rate of production of 0.250 units/day for Task A, 0.286 units/day for Task B, 0.267 units/day for Task C. As presented earlier, the balancing of the lines result in a shorter overall duration of the project.

However, it is important to notice that this is not always a good practice. For example, in a construction project where a skyscraper is the product, or in a smaller scale real estate project, the deliverables cannot be transferred in a “first in-first out” routine. They are transferred to the client in a single batch. Therefore, the measure showed on Exhibit 5 would increase the inventory of completed work. It is possible to see, while examining Exhibit 5 that the first floor would wait 12 days, while the second and third would wait 8 and 4 days respectively, which results in a total of 24 days. The Line of Balance of Exhibit 3 has a total of 18 days, 25% less.

Another relevant consequence of breaking the continuity is that resources will remain for a longer amount of time allocated on the project. On Exhibit 5, the resources of Task 2 would be dedicated to this project for 14 days, while at Exhibit 3 the total time is only 8 days (about 43% less). For Task 3, the modeling pattern of Exhibit 6 results in 15 days of its resources, while the modelling of Exhibit 3 results in 12 days (20% less). This would imply a larger human resources cost for the project due to two main reasons:

• Underutilization of resources, since the crew assigned to task 2 would be idle for 6 days in total. In Brazil, the average labor cost for residential buildings is about 50%, according to indexes published by the Brazilian Chamber of Construction Industry [2]. POPESCU, PHAOBUNJONG and OVARARIN inform that construction projects’ labor costs range from 30 to 50% [11];
• Demobilization and remobilization of crews, that is described by KENLEY & SEPPÄNEN [5] as a source of cost (and mostly schedule) uncertainty in construction projects, especially when the amount of time between demobilization and remobilization is short (one or two weeks). This inefficiency can results in a riskier schedule.

The management team has to study carefully the consequences of breaking the continuity in order to decide what the best option for the project schedule is. The tradeoff between shorter durations and the increase of risk and costs must be taken into consideration.

It is relevant to point out that describing the entire potential of the LBSM is not the purpose of this paper. The examples presented here are extremely simplified usages in order to demonstrate a still considerably unknown scheduling method and how it can optimize schedules.

Now that we have evaluated how the LBSM functions, we are able to propose two directions for the modelling to occur: the network approach and the linear scheduling approach. The difference between these approaches is the use of the CPM network calculations – the first, Network Approach, accepts CPM, while the second, Linear Schedule Approach, does not.

The Network Approach

It is important to observe the situation shown on Exhibit 3, where two sequential tasks show different rates of progress. Task 1 has 4 days of duration and its successor, Task 2, has 2 days, which means that the Task 1 progression has a smaller slope than the Task 2 progression (meaning that it is slower). Modeling the cycle of the continuous repetition of Task 1 can be done by using the standard “FS” (finish-start) relation, since the next task initiates immediately after the working crew ends the task on the preceding production unit.

To allow the same continuity for Task 2, it is necessary to base the modeling of its cycle at the end of the last repetition of Task 1. Task 1 on the fourth floor already has a “FS” relation with Task 2 on the fourth floor. This way, the start date of Task 2 at the fourth floor is well defined on time. The described sequence is detailed in Exhibit 6.

Exhibit 6 – Network Diagram With the Logical Relationship Between Tasks

Modeling the preceding repetitions of Task 2 on the lower floors using the “FS” relationship is not sufficient to ensure that the work can be performed continuously and efficiently. The only way to ensure this is by using a different logical linkage, one that can transfer the constraint defined by the cycle of repetition of Task 1 “downward” from Task 2 on the fourth floor to Task 2 on the first floor. Therefore, with the definition by the Project Management Institute® (PMI®), the predecessor in this case is Task 2 on the fourth floor, despite the fact that this is currently the final repetition in the schedule; it offers the time constraint for the sequence of tasks. The successor is, then, Task 2 on the third floor – a task that happens earlier than its predecessor does, but has its timing defined by the task that comes next on the time schedule [10].

This relationship between these two tasks is different; the start of the task that happens later in time is connected to the end of the task that happens immediately before. This represents a legitimate “start-finish” relation. The result is that the start of Task 2 on the fourth floor is linked to the end of Task 2 on the third floor that has its start linked to the end of Task 2 on the second floor that has its start linked to the end of Task 2 on the first floor (Exhibit 8). Note that Task 2 on the second floor has two predecessors, a “finish-start” link from Task 1 on the second floor, and a “start-finish” link from Task 2 on the third floor.

Exhibit 7 – SF Relation Between the Repetitions of Task 2

As we continue to model the network diagram, the fourth floor is no longer the time constraint for the cycle of the next set of tasks. From Exhibit 3, it is possible to perceive that the Task 3 progression has a slope that is smaller than the Task 2 progression (in other words, it is slower). To maintain a continuous, uninterrupted progression for Task 3, it must proceed from the end of Task 2 on the first floor “upwards” (from the first until the fourth floor). This sequence can therefore be modeled by using the “FS” relation, connecting the end of Task 3 on the first floor with the start of Task 3 on the second floor, which has its end linked with the start of Task 3 on the third floor. Finally, Task 3 on the third floor has its end linked with the start of Task 3 on the fourth floor.

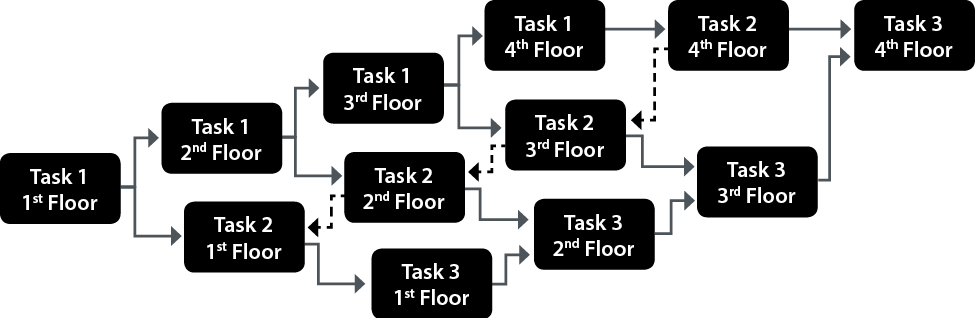Exhibit 8 – Complete Network Diagram for the Example

A peculiarity can be observed when modeling this network diagram using CPM schedule management software in order to identify the critical path. The result displayed by Microsoft® Project states that every single task on the network is part of the critical path. Analyzing the progression of Task 2, it is true to say that every delay on a task will delay the following repetition. Although, we can observe in Exhibit 9 that there will be no delay on the project end date if Task 2 on the second floor has a one-day delay. In the same way, Task 2 on the third floor can absorb a two-day delay and Task 2 on the fourth floor can absorb a three-day delay without affecting the project completion date.

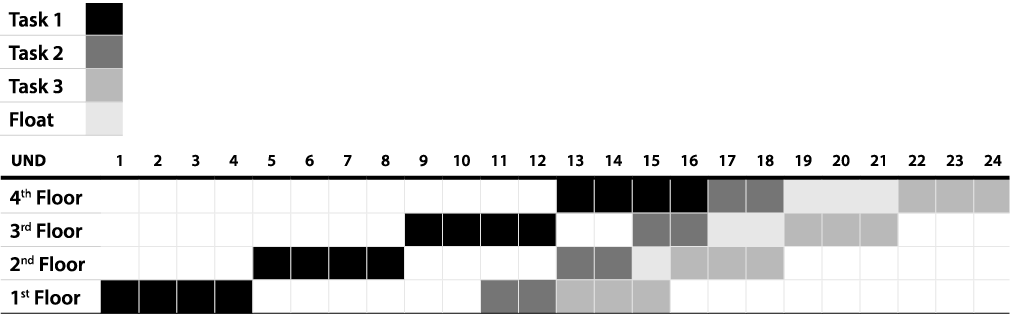Exhibit 9 – Total Float for the Repetitions of Task 2

On the PMBOK (9), the critical path is “normally characterized by zero total float”, while the definition of “total float” is “the amount of time that a schedule activity can be delayed or extended from its early start date without delaying the project finish date or violating a schedule constraint”. Mubarak (7), in turn, consider the critical path as a “continuous chain of critical activities from the start to the end of the project”, defining “critical activities” as activities that can suffer no delay without delaying the project as well. The same is present on the work of Kerzner (6): “there is no slack time in any of the events on this (critical) path”.

There is no doubt that the path shown by the software is, indeed, the critical path, since the path duration is equal to the project duration (this is also a characteristic of the critical path recognized by the authors cited above). Still, it should be noted that the inclusion of the “SF” relation on network diagrams reveals an “unexpected result”. Although the Microsoft® Project (the software used) display a clear critical path in terms of project duration, there are “hidden” floats on the network. Thus, the downside of this approach is that the CPM calculations regarding floats will not suffice, demanding a manual analysis of the floats present at the schedule and how it can be used

There is a difference between modelling this schedule with the “FS” relationship and the constraint “As Late As Possible” – “ALAP”. The Exhibit 10 shows the schedule designed only with “FS” relationships and the “As Late as Possible” constraint.

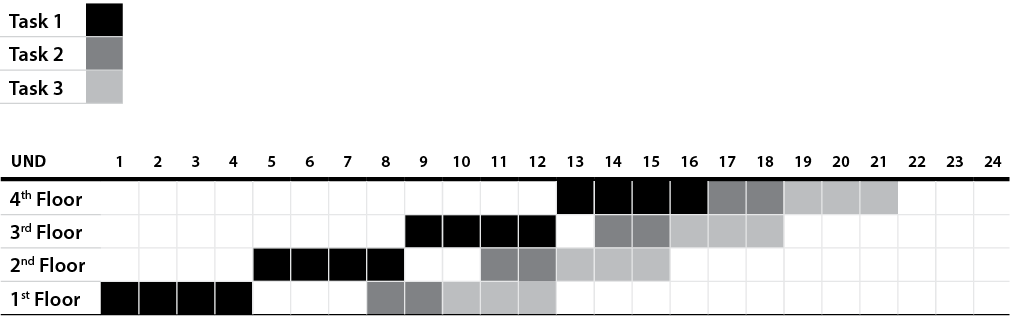Exhibit 10 – Line of Balance Resulted from “FS” Relation and “ALAP”

It is possible to perceive that the Line of Balance is similar to the one at the Exhibit 5, in terms of duration, but with only one discontinuous task progression. The risk of schedule and cost related to the discontinuity remains and the resources for Task 2 progression remain assigned for a longer period. In addition, the Line of Balance above has the same inventory of completed work that the one presented on Exhibit 3.

It is important to note that the logical structures applied resulted in Line of Balances suitable to different set of contexts. The structure constructed with “SF” relationships will result in continuous lines, not susceptible to any risks related to discontinuity. The other logical structure, with “FS” relationships and “ALAP”, will result in a shorter duration of the project with a higher risk exposure trade-off. In sum, both “SF” and “FS” + “ALAP” structures are valid for modelling a LB with a CPM software.

The management team, knowing the particularities of each model, will have to decide which one fits more properly to the project’s context. If the risks associated with task discontinuity are worth taking in order to achieve scheduled duration reduction, the “FS” + “ALAP” structure should by applied. In cases where those risks are not worth taking, the “SF” structure should be preferred. In fact, a larger and more complex schedule may offer situations where both structures are present.

The Linear Schedule Approach

This approach uses the CPM software as a graphical tool for designing the lines and controlling the project along its life cycle, focusing only on the fundamentals of the method: the rate of production of each line and the balancing of all of them. The result, instead of a network, is a graph similar to the one presented in the Exhibit 11.

Exhibit 11 – The Linear Schedule Approach

Exhibit 11 shows each line as the representation of the progression of six repetitive tasks in a construction project. This methodology ignores the creation of a completely connected CPM network, focusing only on the design of the lines and then tuning them to an efficient configuration – meaning adjusting the distance between the lines and further balancing them. This proposition is not at all disconnected from the reality of project management in the construction industry, given that only 14% of respondents work with a fully linked CPM schedule, according to a survey performed in the UK [13].

This utilization is, in truth, a consequence of the definition of Line of Balance per se. Additionally, it benefits from the main idea behind the first methodology, that is to subordinate a sequence of tasks to an imposed time constraint. In the example given, the finishing date of the cycle of Task 1 imposes a fixed date to the end of the cycle of Task 2 (both lines becoming “linked at the top”). This approach focus on subordinating the sequence of repetition to a milestone.

On the subject of milestones, a practical example would be finishing a sequence of painting activities for a building by the end of the sixth month of the project, or the completion of the management plan should be by the third month after the project approval. Assuming that milestones in a network diagram are tasks with zero duration and with a fixed start date, the modeling of one of the examples is presented in Exhibit 12.

Exhibit 12 – Milestones and SF Relation

Exhibit 12 shows that Milestone 1 subordinates the end of the workflow of the painting activities. This way, the continuous use of SF relationships between the tasks’ repetitions moving “downwards” will result in the necessary start date for the workflow. Equally, the sequencing may take its start on a milestone representing the beginning of the painting tasks, when the sequence is modelled “upwards” with the usual “FS” relationship. The example of the following is presented in the next Exhibit, where a sequence of sections of earthwork is subordinated to a milestone.

Exhibit 13 – Milestones and FS Relation

If the management team decides to schedule a non-continuous task progression, after considering the uncertainties and negative consequences, the line can be modelled using lags or leads. If the management team was to model the Earthwork task progression with a two-day lag between each section, it could be done like in the Exhibit 14.

Exhibit 14 – Non-continuous Task Progression

Thus, a milestones chart, defined by the experience and lessons learned from previous projects or with expert judgment, for instance, can be used to initiate the process. The proposed methodology deals with either starting dates milestones and delivery dates milestones.

At this approach, the schedule control’s main goal is to prevent the clash between lines. The clash represents a rupture on the project workflow. Despite the fact that this modelling rejects the assignment of predecessors, the hard-logic relationships among the tasks remains. Accordingly, if a line “invades” another, one of the work crews will have to become idle until the situation is remediated or will have to be transferred. This can happen for either a line that is progressing with a higher speed than anticipated or a line that is progressing slower.

Without the CPM calculations, the control is done, in other words, only by the flow of work of the construction project as a whole. The clash is a consequence of an unbalanced execution, with task progressions going off track. Other consequence of lacking the CPM calculation is, evidently, that the management team experiences a paradigm shift. The CPM method delivers a clear priority for team: the critical path. The workflow perspective assigns to every single line the same rank of priority. The focus of the management team will derive from the information gathered from the execution.

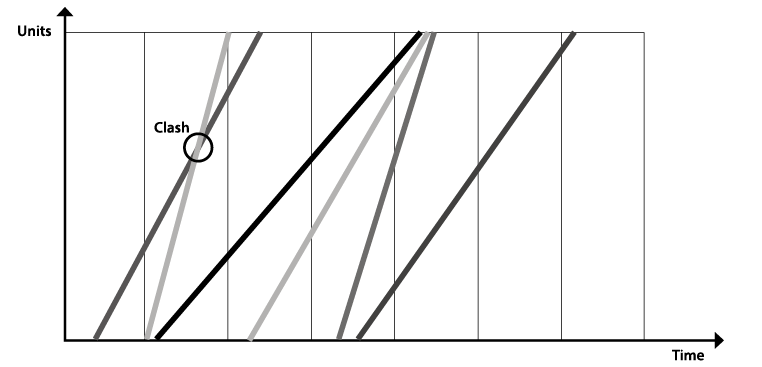Exhibit 15 – Lines Clashing

Conclusion

This paper proposed the utilization of CPM software (as seen, the most largely used) as a tool for the Line of Balance Scheduling Method. Inherently, the CPM and the LBSM are different from each other. CPM, according to Kenley and Seppänen (5), focuses on how discrete activities connect to each other in order to identify the critical path. LBSM focuses on the perspective of flow of work, when the scheduling planning concerns with the production process of the particular production units (seemingly to designing a “factory”). Still, the scarcity of commercial software that covers its fundamentals is pointed as a barrier to its implementation and the CPM commercial software may supply a preliminary solution.

On the subject of the model, the paper proposed that the use of the “SF” relation could be of value for the modelling. The LBSM, its behavior, and its peculiarities were discussed first and then two approaches for the modelling were proposed: the Network Approach and the Linear Scheduling Approach. Both were discussed and exemplified.

The first approach allowed the Line of Balance to be modelled as a CPM network. The continuous progression of tasks, as demonstrated, can be represented with the use of the “SF” relationship when the lines become “linked at the top”. On the other hand, this usage implies on some “unexpected results” regarding the critical path, demanding further investigation from the management team for the situation of floats on the lines. The lines can be modelled with “FS” relationships and the “As Late as Possible” constraint as well, but the result does not guarantee the continuity of the task repetitions, exposing the project to risks related to work discontinuity. On the other hand, the resulting LB presented a shorter duration than the one structured with “SF” relationships. Both structures generated consistent results that may be valuable for different project contexts and even can be combined with more complex project schedules. Thus, it is the management team’s decision which structure is more suitable for the project.

The second approach behavior accordingly with the definition of LBSM. The CPM calculation routine were dropped completely and the CPM software was used as a graphical tool for designing the lines that represent the task progressions and their control over the project life cycle. The “SF” relation employed a mean to subordinate the tasks to a delivery milestone, while the common “FS” relation was used to build the sequence from a start milestone. Connecting the task sequences to a milestone allows the scheduler to move them on the time scale with the goal of tuning the schedule and further balancing.

Bibliography