• Oct 09, 2010
• 4,741 views
• Short URL: rvarg.as/nm/

Utilizando el Proceso Analítico Jerárquico (PAJ) Para Seleccionar y Priorizar Proyectos en una Cartera

Resumen

El objetivo de este trabajo es presentar, discutir y aplicar los principios y técnicas del Proceso Analítico Jerárquico (PAJ) en la priorización y selección de proyectos de una cartera. El PAJ es uno de los principales modelos matemáticos actualmente disponibles para apoyar la teoría de la decisión.

Cuando observamos la forma en que las organizaciones deciden qué proyectos ejecutar, podemos notar un constante deseo de contar con criterios claros, objetivos y matemáticos (Haas & Meixner, 2005). Sin embargo, la toma de decisiones es, en su totalidad, un proceso cognitivo y mental derivado de la selección más adecuada posible en función de criterios tangibles e intangibles (Saaty, 2009), que se eligen arbitrariamente por quienes toman las decisiones.

Este documento también habla de la importancia y de algunos posibles criterios para la priorización de proyectos y, mediante el uso de un ejemplo ficticio de priorización, demuestra el PAJ paso a paso, mostrando las prioridades resultantes y determinando las posibles inconsistencias.

La Importancia de la Selección de Proyectos y de la Priorización

Uno de los principales desafíos que enfrentan las organizaciones hoy en día reside en su capacidad para elegir las alternativas más correctas y consistentes, de tal manera que se mantenga la alineación estratégica. Dada una situación específica, tomar las decisiones correctas es probablemente uno de los retos más difíciles para la ciencia y la tecnología (TRIANTAPHYLLOU, 2002).

Si tenemos en cuenta la dinámica cambiante del entorno actual, como nunca hemos visto antes, tomar las decisiones correctas basadas en objetivos adecuados y alineados constituye un factor crítico, incluso para la supervivencia de la organización.

Básicamente, la priorización de los proyectos en una cartera no es más que un plan de ordenación basado en una relación coste-beneficio de cada proyecto. Los proyectos con mayores beneficios en comparación con sus costes, tendrán una prioridad más alta. Es importante observar que una relación coste-beneficio no significa necesariamente el uso exclusivo de criterios financieros, como el ampliamente conocido ratio coste-beneficio, en lugar de un concepto más amplio de los beneficios derivados de la ejecución del proyecto y sus actividades relacionadas.

Dado que las organizaciones pertenecen a un contexto complejo y variable, muchas veces incluso caótico, el reto de la definición antes mencionada reside precisamente en la determinación de cuáles son los costes y beneficios para cualquier organización.

Al analizar la tabla anterior, se puede observar que las diferentes dimensiones demuestran lo complejo que es llegar a una traducción exacta del significado de costes bajos y beneficios altos. Esa es la razón por la cual un criterio único o traducción no es lo suficientemente viable como para determinar qué proyecto debe o no debe ser realizado. Por lo tanto, es necesario emplear un análisis de criterios múltiples (TRIANTAPHYLLOU, 2002), que permita tomar decisiones teniendo en cuenta las distintas dimensiones y necesidades de la organización en conjunto.

El estándar del PMI para la Gestión de la cartera (PMI, 2008) dice que el alcance de una cartera de proyectos debe derivar de los objetivos estratégicos de la organización. Estos objetivos deben estar alineados con la hipótesis de que a su vez pueden ser diferentes para cada organización. En consecuencia, no existe un modelo perfecto que cubra los criterios correctos a ser utilizados para cualquier tipo de organización para establecer prioridades y seleccionar proyectos. Los criterios utilizados por la organización deben basarse en los valores y preferencias de los responsables de la decisión.

Criterios Actuales Utilizados en la Priorización de Proyectos

Aunque las decisiones se basan en los valores y preferencias de los que toman la decisión, al mismo tiempo se pueden utilizar un conjunto de criterios u objetivos específicos para priorizar los proyectos y determinar el verdadero significado de una relación óptima entre costes y beneficios.

Los principales grupos de criterios son los siguientes:

Financiero – Un grupo de criterios con el objetivo de capturar los beneficios financieros de los proyectos. Están directamente relacionados con la medición de los costes, la productividad y el beneficio. Algunos ejemplos son:

• Retorno de la Inversión (ROI, Return on Investment) – Es el porcentaje del margen de beneficio del proyecto. Permite comparar el rendimiento financiero de los proyectos con las diferentes inversiones y ganancias.
• Beneficios (moneda) – El valor (en moneda) de los beneficios financieros obtenidos por el proyecto. Un proyecto puede tener un retorno de la inversión más pequeño, pero su ganancia nominal puede ser mayor.
• Valor Actual Neto (VAN – NPV, Net Present Value) – Es la diferencia entre los beneficios y costes del proyecto teniendo en cuenta que todos los ingresos y gastos se valoran a la fecha actual. Con el fin de hacerlo, es necesario traer todos los valores futuros a la fecha actual mediante el uso de un tipo de interés. Esto permite la evaluación y la comparación entre los proyectos que tienen ingresos y gastos futuros en diferentes períodos de tiempo.
• Plazo de recuperación (Payback) – Es la cantidad de períodos de tiempo necesaria para recuperar todas las inversiones originales del proyecto.
• Beneficios financieros / Tasa de Costes – Es la relación entre el valor actual de los beneficios y el valor actual de los costes. Cuanto más alto sea el ratio, más viable es el proyecto bajo la perspectiva de la relación coste / beneficio.

Estratégico – Un grupo de criterios directamente relacionados con los objetivos estratégicos de la organización. Los criterios/objetivos estratégicos están determinados por los métodos utilizados para la estrategia corporativa en cascada como el Cuadro de Mando Integral. Se diferencian de los criterios financieros porque son criterios estratégicos específicos para cualquier organización. Las organizaciones con diferentes estrategias sin duda tienen diferentes criterios de priorización. Algunos ejemplos pueden ser la mejora de la capacidad para competir en los mercados internacionales, el uso de prácticas ecológicas, optimizar los procesos internos, reducir los gastos en comparación con los competidores de referencia, mejorar la reputación de los productos y servicios, etc.

Riesgos (amenazas) – Se determina el nivel de tolerancia al riesgo que una organización acepta en la ejecución de un proyecto. Los criterios basados en la evaluación del riesgo de tipo amenaza también pueden incorporar la evaluación de las oportunidades (Hilson, 2003). Sin embargo, muchas veces se puede observar que la evaluación de las oportunidades de un proyecto ya están cubiertas y atendidas por los criterios estratégicos. Otra perspectiva igualmente posible para este criterio enlaza con el riesgo que supone para la organización la no realización del proyecto.

Urgencia – Se determina el nivel de urgencia del proyecto. Los proyectos considerados urgentes requieren decisiones y acciones inmediatas y, por lo tanto, tienen una mayor prioridad que los proyectos que no son urgentes.

Compromiso de los interesados – Un grupo de criterios que tiene como objetivo evaluar el nivel de compromiso de los interesados hacia el proyecto. Cuanto mayor sea el compromiso con el proyecto mayor prioridad recibe el proyecto. El compromiso puede ser evaluado de una manera amplia, donde todos los actores son considerados como un grupo único o puede ser descompuesto en diferentes grupos de interés, como por ejemplo:

• Compromiso del cliente
• Compromiso de la comunidad
• Compromiso de la organización
• Organismos reguladores
• Compromiso del equipo de proyecto
• Compromiso del director de proyecto

Conocimiento técnico – Evalúa los conocimientos técnicos necesarios para realizar el proyecto. Cuanto más conocimiento técnico disponible más fácil será realizar un determinado proyecto y, en consecuencia, hará que el proyecto utilice menos recursos. Es importante señalar que, si es necesario establecer criterios y objetivos relacionados con el proceso de aprendizaje y crecimiento, estos criterios deben ser asociados a los criterios estratégicos de la organización y no con ningún conocimiento técnico.

Proceso Analítico Jerárquico

La programación multicriterio, a través del uso del Proceso Analítico Jerárquico, es una técnica para la toma de decisiones en entornos complejos donde se consideran muchas variables o criterios en la priorización y selección de alternativas o proyectos.

El PAJ se desarrolló en los años 70 por Thomas L. Saaty y ha sido desde entonces estudiado ampliamente, siendo utilizado actualmente en la toma de decisiones en escenarios complejos, donde las personas trabajan juntas para tomar decisiones cuando las percepciones humanas, los juicios y las consecuencias tienen una repercusión a largo plazo (Bhushan y la RAI, 2004).

La aplicación del PAJ se inicia con un problema que se descompone en una jerarquía de criterios con el fin de ser más fácil de analizar y comparar de manera independiente (Figura 1). Después de que se construya esta jerarquía lógica, los que toman la decisión puedan evaluar sistemáticamente las alternativas al hacer comparaciones entre pares para cada uno de los criterios elegidos. Esta comparación puede utilizar los datos concretos de las alternativas o juicios humanos como una forma de entrada de información subyacente (Saaty, 2008).

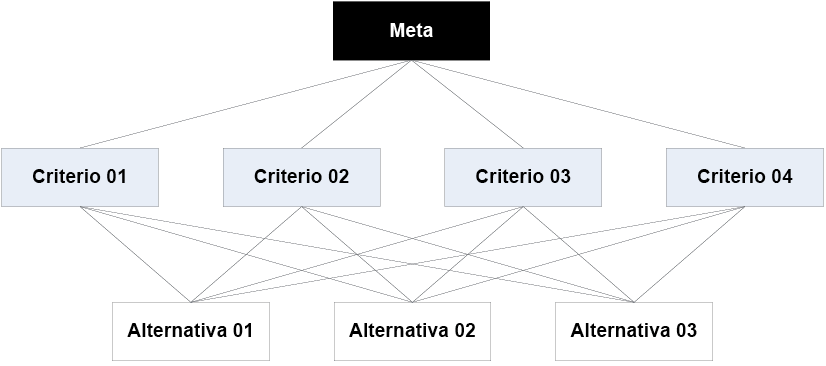Figura 1 – Ejemplo de una jerarquía de criterios / objetivos

El PAJ transforma las comparaciones, que son la mayoría de las veces empíricas, en valores numéricos que son procesados y comparados. El peso de cada factor permite la evaluación de cada uno de los elementos dentro de la jerarquía definida. Esta capacidad de convertir los datos empíricos en modelos matemáticos es la principal contribución distintiva de la técnica PAJ cuando se contrasta con otras técnicas de comparación.

Una vez que se han hecho todas las comparaciones y se han establecido los pesos relativos entre cada uno de los criterios a ser evaluados, se calcula la probabilidad numérica de cada alternativa. Esta probabilidad determina la probabilidad que tiene la alternativa para cumplir con la meta propuesta. Cuanto mayor sea la probabilidad, más posibilidades tiene la alternativa para satisfacer la meta final de la cartera.

El cálculo matemático que implica el PAJ puede parecer simple al principio, pero cuando se trata de casos más complejos, los análisis y los cálculos se hacen más profundos y más exhaustivos.

La Escala de Ccomparación (Escala de Saaty)

La comparación entre dos elementos utilizando el PAJ se puede hacer de diferentes maneras (TRIANTAPHYLLOU y Mann, 1995). Sin embargo, la escala de importancia relativa entre dos alternativas sugeridas por Saaty (Saaty, 2005) es la más utilizada. Al atribuir valores que varían de 1 a 9, la escala determina la importancia relativa de una alternativa cuando se compara con otra alternativa, como podemos ver en la Tabla 1.

Es común utilizar siempre los números impares de la tabla para asegurarse de que existe una diferencia razonable entre los puntos de medición. El uso de los números pares sólo debe adoptarse si hay una necesidad de negociación entre los evaluadores. Cuando no se puede alcanzar un consenso natural se plantea la necesidad de determinar un punto medio en la solución negociada (compromiso) (Saaty, 1980).

La matriz de comparación se construye a partir de la escala de Saaty (Tabla 2).

Un Ejemplo de la Aplicación del PAJ en una Cartera

Con el fin de servir como ejemplo de los cálculos del PAJ para la priorización de proyectos se ha elegido el desarrollo de un modelo de decisión para la organización ficticia ACME. El ejemplo desarrolla más adelante los conceptos, términos y enfoques del PAJ que se discutirán y analizarán.

El primer paso para construir el modelo del PAJ consiste en la determinación de los criterios que se utilizarán. Como ya se mencionó, cada organización desarrolla y estructura su propio conjunto de criterios, que a su vez deben estar alineados con los objetivos estratégicos de la organización.

Para nuestra organización ficticia ACME vamos a suponer que se ha realizado un estudio junto con las áreas Finanzas, Planificación Estratégica y Dirección de Proyectos sobre los criterios que se utilizarán. Se ha aceptado el siguiente conjunto de 12 (doce) criterios y se han agrupado en 4 (cuatro) categorías como se muestra en la jerarquía de la figura 2.

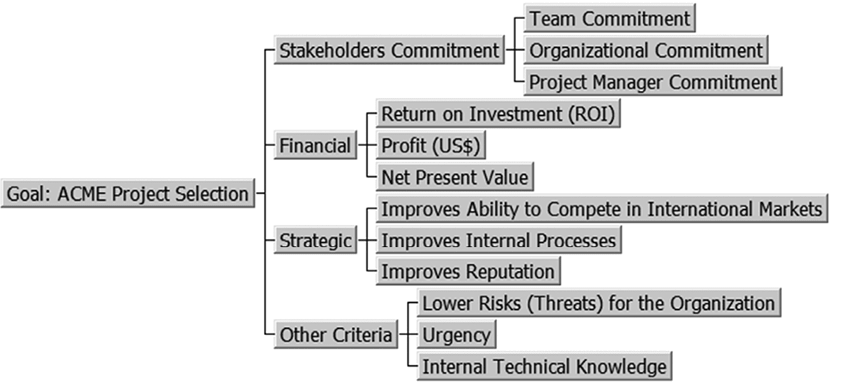Figura 2 – Jerarquía de los criterios para la organización ficticia ACME

Determinación de la Matriz de Comparación, el Vector de Prioridad (autovector) y la Inconsistencia

Después de que se ha establecido la jerarquía, los criterios deben ser evaluados por pares con el fin de determinar la importancia relativa entre ellos y su peso en relación con la meta global.

La evaluación comienza por determinar el peso relativo de los grupos de criterios iniciales (Figura 3). La Tabla 3 muestra los datos del peso relativo entre los criterios que han sido determinados por los que toman las decisiones en ACME.

Figura 3 – Grupo inicial de criterios/objetivos de ACME

Con el fin de interpretar y dar peso relativo de cada criterio, es necesario normalizar la matriz de comparación anterior. La normalización se realiza dividiendo cada valor de la tabla por el total del valor de la columna total (Tabla 4).

La contribución de cada criterio a la meta de la organización está determinado por los cálculos realizados utilizando el vector de prioridad (o autovector). El autovector muestra el peso relativo entre cada criterio obtenido de forma aproximada calculando la media aritmética de todos los criterios, tal como se muestra en el Cuadro 10. Podemos observar que la suma de todos los valores del vector es siempre igual a uno (1). El cálculo exacto del autovector se determina sólo en casos específicos. Esta aproximación se aplica la mayoría de las veces con el fin de simplificar el proceso de cálculo, ya que la diferencia entre el valor exacto y el aproximado es menos del 10% (KOSTLAN, 1991).

Para fines de comparación, se ha utilizado una aplicación de software matemático para calcular el valor exacto para el vector mediante el uso de matrices potenciales. Los resultados se muestran en la Tabla 6.

Se puede observar que los valores aproximados y exactos se encuentran muy cerca el uno del otro, por lo que el cálculo del vector exacto requiere de un esfuerzo matemático que se puede eximir (KOSTLAN, 1991).

Los valores hallados en el autovector tienen un significado físico directo en el PAJ. Determinan la participación o el peso de este criterio en relación con el resultado total de la meta. Por ejemplo, en nuestra organización ACME, los criterios estratégicos tienen un peso del 46% 0,04 (cálculo exacto del autovector) en relación con la meta total. Una evaluación positiva de este factor contribuye aproximadamente con 7 (siete) veces más que una evaluación positiva en el criterio de compromiso de los interesados (peso 6,84%).

El siguiente paso es buscar las inconsistencias de datos. El objetivo es capturar la información suficiente para determinar si los que toman las decisiones han sido consistentes en sus decisiones (TEKNOMO, 2006). Por ejemplo, si los que toman las decisiones afirman que los criterios estratégicos son más importantes que los criterios financieros y que los criterios financieros son más importantes que los criterios de compromiso de los interesados, sería inconsistente afirmar que los criterios de compromiso de los interesados son más importantes que los criterios estratégicos (si A> B y B> C no sería coherente decir que A<C).

El índice de inconsistencia se basa en máximo autovalor, que se calcula sumando el producto de cada elemento del vector (Tabla 5) por el total de la columna correspondiente de la matriz de comparación original (Tabla 4). La Tabla 7 muestra el cálculo del máximo autovalor de Máximo Autovalor (λMax)1

1 Los valores del autovector utilizados a partir de ahora se basarán en los valores exactos y no en los valores aproximados, ya que se han calculado los valores exactos y por tanto están disponibles.

.

El cálculo del índice de consistencia (Saaty, 2005) está dado por la siguiente fórmula

Donde IC es el Índice de Consistencia y n es el número de criterios evaluados.

Para nuestra organización ACME, el índice de consistencia (IC) es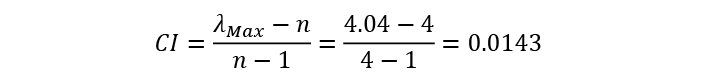

Con el fin de verificar si el índice de consistencia (IC) es el adecuado, Saaty (Saaty, 2005) sugiere lo que se ha denominado Tasa de Consistencia (TC, CR Consistency Rate), que se determina por la relación entre el índice de consistencia y el índice de consistencia aleatorio (IA – RI, Random Consistency Index). La matriz se considera coherente si la ratio resultante es inferior al 10%.

El valor del IA es fijo y se basa en el número de criterios evaluados, como se muestra en la Tabla 8

Para nuestra organización ACME, la tasa de consistencia para el grupo de criterios iniciales es

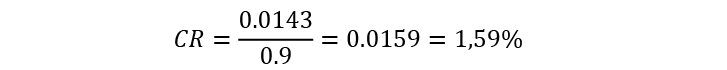
Ya que su valor es inferior al 10%, la matriz puede ser considerada como consistente. Los criterios de prioridad resultantes para el primer nivel se pueden ver en la Figura 4.

Figura 4 – Resultados de la matriz de comparación para el grupo de criterios de ACME, demostrando la contribución de cada criterio a la meta definida para la organización

Al observar la Figura 4 y los autovectores, es evidente que los criterios estratégicos tienen un aporte a la meta del 46,04% mientras que los criterios de compromiso de los interesados contribuyen a la meta con el 6,84%.

Otros Cálculos que Implican los Criterios Elegidos

Al igual que se hizo con el grupo de criterios iniciales para la organización de ACME, es necesario evaluar el peso relativo de los criterios para el segundo nivel de la jerarquía (Figura 5). Este proceso se ejecuta al igual que el paso para evaluar el primer nivel de la jerarquía (grupo de criterios) como se mostró antes.

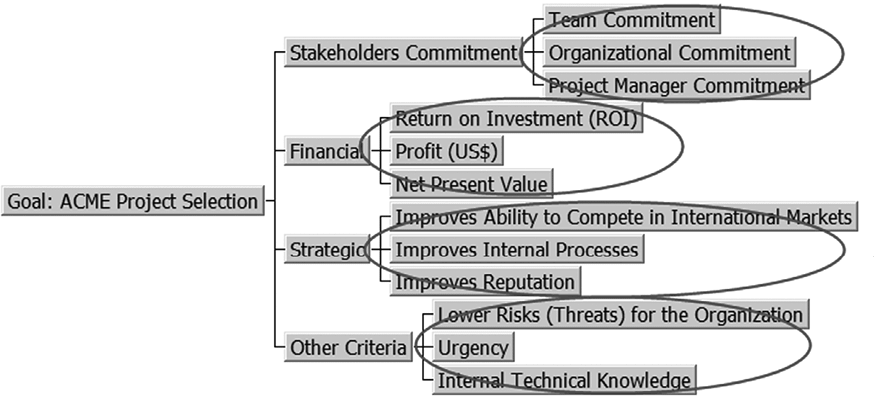Figura 5 – Jerarquía de los criterios para la organización ficticia ACME destacando el segundo nivel jerárquico

Las siguientes tablas muestran las matrices de comparación de los criterios con las comparaciones por pares ya adoptadas por los que toman las decisiones.

Los gráficos siguientes (Figura 6 a 9) muestran los resultados de prioridad para los subcriterios para cada uno de los grupos de criterios2

2 Los datos han sido simulados y calculados utilizando ExpertChoice 11.5 para Windows, disponible en www.expertchoice.com

y sus respectivos índices de inconsistencia. Podemos observar que ninguno de los criterios demuestra incoherencia por encima de los límites tolerables.

Figura 6 – Resultados de prioridad para los criterios de compromiso de los interesados

Figura 7 – Resultados de prioridad para los criterios financieros

Figura 8 – Resultados de prioridad para los criterios estratégicos

Figura 9 – Resultados de prioridad para los otros criterios

La prioridad global para cada criterio se determina por el resultado de la multiplicación de cada prioridad en el primer nivel por su respectiva prioridad en el segundo nivel. Los resultados se muestran en la jerarquía de la Figura 10. También podemos ver que la suma de los pesos de los doce (12) factores es igual a 1.

Figura 10 – Jerarquía de los criterios para la organización ficticia ACME con las prioridades globales para cada criterio

Evaluación de los Proyectos Candidatos a la Cartera

Después de haber estructurado el árbol y estableció los criterios de prioridad, ahora es posible determinar cómo se ajusta cada uno de los proyectos candidatos a los criterios elegidos. De la misma manera que se ha hecho la priorización de criterios, los proyectos candidatos son comparados en pares con cuidado teniendo en cuenta todos los criterios establecidos.

Para nuestra organización ACME, se han identificado seis (6) proyectos que deben ser priorizados. Los proyectos ficticios son:

• Trasladarse a una nueva oficina
• Nuevo sistema ERP
• Apertura de una oficina en China
• Desarrollo de un nuevo producto destinado al mercado internacional
• Infraestructura de IT para outsourcing
• Nueva campaña local de marketing

Para la aplicación del PAJ, los que toman las decisiones en la organización ACME han comparado seis (6) proyectos teniendo en cuenta cada uno de los doce (12) criterios establecidos. Los resultados se muestran en las siguientes doce (12) tablas.

Después de calcular todas las prioridades y los índices de inconsistencia, es posible determinar el peso relativo de cada proyecto para cada criterio, como podemos ver en los siguientes doce (12) diagramas (un gráfico para cada criterio)

Figura 11 – PResultados de prioridad para los proyectos de acuerdo con el criterio compromiso del equipo

Figura 12 – Resultados de prioridad para los proyectos de acuerdo con el criterio compromiso de la organización

Figura 13 – Resultados de prioridad para los proyectos de acuerdo con el criterio compromiso del director de proyecto

Figura 14 – Resultados de prioridad para los proyectos de acuerdo con el criterio retorno de la inversión

Figura 15 – Resultados de prioridad para los proyectos de acuerdo con el criterio beneficios (en dólares de EE.UU.)

Figura 16 – Resultados de prioridad para los proyectos de acuerdo con el criterio valor actual neto

Figura 17 – Resultados de prioridad para los proyectos de acuerdo con el criterio mejorar la capacidad de competir en los mercados internacionales

Figura 18 – Resultados de prioridad para los proyectos de acuerdo con el criterio mejorar los procesos internos

Figura 19 –Resultados de prioridad para los proyectos de acuerdo con el criterio mejorar la reputación

Figura 20 – – Resultados de prioridad para los proyectos de acuerdo con el criterio reducir los riesgos (amenazas) para la Organización

Figura 21 – Resultados de prioridad para los proyectos de acuerdo con el criterio urgencia

Figura 22 – Resultados de prioridad para los proyectos de acuerdo con el criterio conocimientos técnicos internos

El producto cruzado de todas las evaluaciones de los proyectos con todos los criterios determina la prioridad final para cada proyecto en relación a la meta deseada.

El mecanismo para el cálculo de la prioridad final es la suma de los productos de la multiplicación del peso de cada criterio de prioridad por su peso alternativo.

Para ejemplificar este proceso, la Tabla 25 muestra el proceso de cálculo para la alternativa “Trasladarse a una nueva oficina”

El mismo proceso se debe repetir para los otros cinco (5) proyectos. Los resultados finales de todos los proyectos se muestran en la Figura 23.

Figura 23 – Resultados finales de prioridad para la cartera de proyectos de ACME

La Figura 23 muestra que el proyecto con mayor nivel de cumplimiento de la meta definida es “Desarrollo de un nuevo producto destinado al mercado internacional”. Contribuye con el 34,39% (0,3439). A fin de ilustrar mejor la importancia de la diferencia entre el peso y las prioridades de cada proyecto, este proyecto contribuye con cerca de tres (3) veces más a la meta que el proyecto nueva campaña local de marketing que contribuye con sólo el 13,1% (0,131) a la meta global.

Conclusión

El PAJ ha estado atrayendo la atención de muchos investigadores, principalmente debido a las características del método matemático y el hecho de que es bastante simple producir la entrada de datos (TRIANTAPHYLLOU y Mann, 1995). Su simplicidad se caracteriza por la comparación por pares de las alternativas de acuerdo a criterios específicos (Vargas, 1990). Su aplicación a la selección de los proyectos de la cartera permite a los que toman decisiones contar con una herramienta de soporte de decisiones específica y matemática. Esta herramienta no sólo admite y califica las decisiones sino que también permite su realización para justificar la decisión tomada, así como simular posibles resultados.

El uso del PAJ también supone la utilización de una aplicación de software diseñada específicamente para realizar los cálculos matemáticos. La intención de este documento ha sido mostrar los cálculos principales realizados durante el análisis, permitiendo a los directores de proyecto tener una comprensión adecuada de la técnica, así como de la complejidad para realizar los cálculos manualmente (en el caso de que no se puedan utilizar aplicaciones software).

Otro aspecto importante es la calidad de las evaluaciones realizadas por los que toman las decisiones (Coyle, 2004). Para que una decisión sea lo más adecuada posible debe ser consistente y coherente con los resultados de la organización. Hemos visto que la coherencia de los resultados puede calcularse a través del índice de inconsistencia. Sin embargo, el índice de inconsistencia sólo permite la evaluación de la consistencia y la regularidad de las opiniones de los que toman las decisiones y no si estos complementos son los más adecuados para un contexto de organización específico.

Finalmente, es importante destacar que la toma de decisiones presupone una comprensión más amplia y compleja del contexto que la utilización de una técnica específica. Se predica que la decisión acerca de una cartera es fruto de la negociación, los aspectos humanos y el análisis estratégico, donde los métodos como el PAJ favorecen y guían la realización del trabajo, pero no pueden y no deben ser utilizados como un criterio universal.

Referencias

BHUSHAN, N. & RAI, K. (2004). Strategic Decision Making: Applying the Analytic Hierarchy Process. New York: Springer.

COYLE, G. (2004). The Analytic Hierarchy Process. New York: Pearson Educational.

HAAS, R. & MEIXNER, O. (2005). An Illustrated Guide To Analytic Hierarchy Process. Vienna: University of Natural Resources and Applied Life Sciences.

KOSTLAN, E. (1991). Statistical Complexity of Dominant Eigenvector Calculation. Hawaii: Journal of Complexity Volume 7, Issue 4, December 1991, Pages 371-379. Available at http://www.developmentserver.com/randompolynomials/scdec/paper.pdf

HILLSON, D. (2002). Use a Risk Breakdown Structure (RBS) to Understand Your Risks. San Antonio: PMI Global Congress and Symposium.

PMI (2008). The Standard for Portfolio Management: Second Edition. Newtown Square: Project Management Institute.

SAATY, T. L (1980). The Analytic Hierarchy Process. New York: McGraw-Hill International.

SAATY, T. L. (2005). Theory and Applications of the Analytic Network Process: Decision Making with Benefits, Opportunities, Costs, and Risks. Pittsburgh: RWS Publications.

SAATY, T. L. (2008). Relative Measurement and its Generalization in Decision Making: Why Pairwise Comparisons are Central in Mathematics for the Measurement of Intangible Factors – The Analytic Hierarchy/Network Process. Madrid: Review of the Royal Spanish Academy of Sciences, Series A, Mathematics. Available at http://www.rac.es/ficheros/doc/00576.PDF

SAATY, T. L. (2009). Extending the Measurement of Tangibles to Intangibles. International Journal of Information Technology & Decision Making, Vol. 8, No. 1, pp. 7-27, 2009. Available at SSRN: http://ssrn.com/abstract=1483438

TEKNOMO, K. (2006). Analytic Hierarchy Process (AHP) Tutorial. Available at https://people.revoledu.com/kardi/tutorial/AHP/purchase.html/a>

TRIANTAPHYLLOU, E. & MANN S. H. (1995). Using The Analytic Hierarchy Process For Decision Making in Engineering Applications: Some Challenges. International Journal of Industrial Engineering: Applications and Practice, Vol. 2, No. 1, pp. 35-44, 1995. Available at http://www.csc.lsu.edu/trianta/Journal_PAPERS1/AHPapls1.pdf

TRIANTAPHYLLOU, E. (2002). Multi-Criteria Decision Making Methods: A comparative Study. New York: Springer.

VARGAS, L.G. (1990). An Overview of the Analytic Hierarchy Process and its Applications. European Journal of Operational Research, 48, 2-8.